Александр Артамонов, руководитель группы инженерного анализа и интеграции CAE, Группа «Борлас» (ГК Softline)
В предыдущей статье мы сравнили скорость выполнения расчетов в отечественном комплексе прочностного анализа и теплопереноса CAE Fidesys с иностранными пакетами ANSYS и Nastran и обещали в следующей публикации рассказать про встроенный в него язык макрокоманд. Однако обстоятельства сложились таким образом, что эту статью опередил выход новой версии CAE Fidesys 8.0, новые возможности которой стоят того, чтобы немного изменить планы.
Это мажорная версия. В таких версиях в продукте появляется функционал, существенно расширяющий его возможности. В CAE Fidesys 8.0 компанией-разработчиком реализован большой задел, который находился в разработке и тестировании несколько лет.
В полной мере результат проделанной работы вряд ли возможно оценить в рамках статьи – для этого необходимо длительное использование пакета профессиональными расчетчиками с разной специализацией. Мы сделаем обзор наиболее значимых нововведений.
Начнем с анонса и далее расскажем подробно о каждой функциональности. Итак:
- роторная динамика,
- упруго-пластический расчет оболочек,
- пользовательские сечения балок,
- новый конвертер задач из Nastran,
- инструмент проверки ошибок в расчетной модели до запуска на расчет,
- критерии прочности монослоя композиционного материала.
Если вы не нашли в приведенном списке функционала, который используете в работе, то с большой долей вероятности он уже был в CAE Fidesys до выхода версии 8.0.
А теперь по порядку.
Роторная динамика
В версии CAE Fidesys 8.0 появился расчет задач роторной динамики с учетом гироскопических эффектов.
В предыдущих версиях нельзя было активировать учет эффекта Кориолиса из интерфейса программы, только с помощью команды:
coriolis on
Однако не было возможности учитывать влияние прецессии ротора.
Сейчас учет эффекта Кориолиса и центробежного ускорения доступен в модальном, гармоническом анализе и переходном (временном) процессе. Кроме того, в модальном анализе доступен учет демпфирования. Ранее определение демпфирования было доступно только в гармоническом и временном анализах.
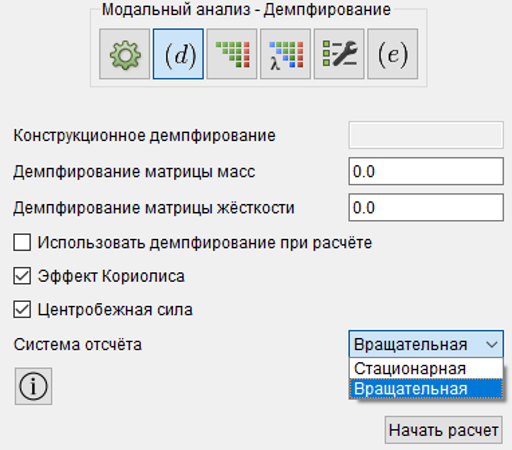
Рисунок 1. Учет гироскопических эффектов и демпфирование в модальном анализе
Решение задачи роторной динамики может быть выполнено во вращательной или стационарной системах координат.
Одной из часто решаемых задач роторной динамики является построение диаграммы Кэмпбелла. В прошлых версиях можно было по результатам нескольких расчетов вручную построить частотную диаграмму – частный случай диаграммы Кэмпбелла. В CAE Fidesys 8.0 построение диаграммы Кэмпбелла с учетом эффекта Кориолиса и центробежного ускорения автоматизировано. Для этого необходимо просто включить опцию в настройках модального анализа и по окончании расчета в постпроцессоре отобразить диаграмму.
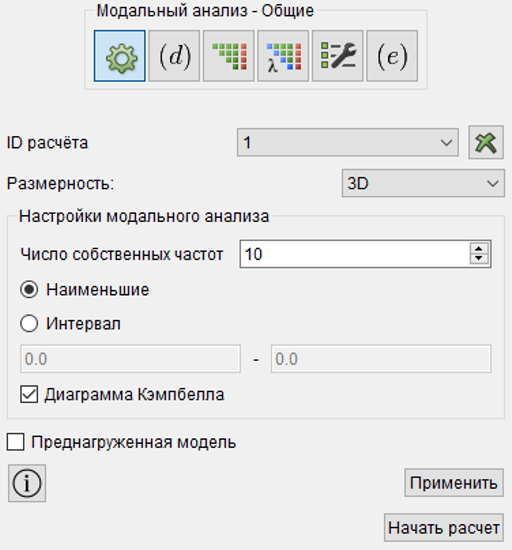
Рисунок 2. Опция «Диаграмма Кэмпбелла» в настройках решателя
Определение угловых скоростей для построения диаграммы Кэмпбелла происходит следующим образом.
Необходимо перейти на Панели команд в Граничные условия и выбрать Угловая скорость.
Включить опцию Диаграмма Кэмпбелла и задать таблицу интересующих скоростей для расчета.
Затем необходимо выбрать ось вращения X, Y или Z и задать отличное от нуля значение в поле напротив. Это значение не является математическим коэффициентом, на который умножаются данные из таблицы скоростей. Это логический фактор для определения оси вращения.
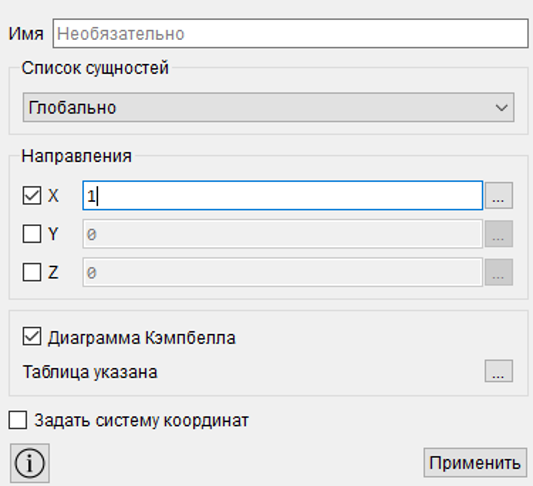
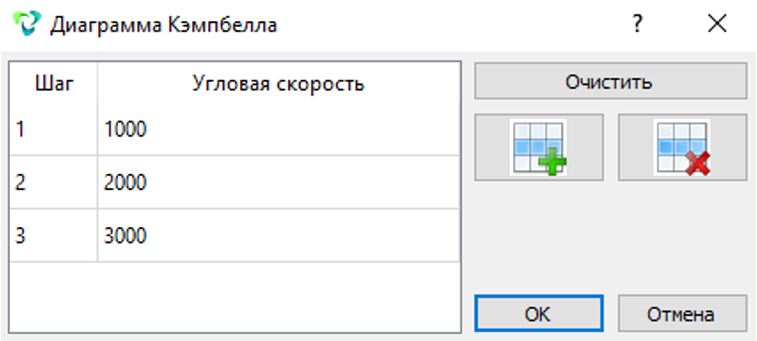
Рисунок 3. Определение скоростей вращения ротора для диаграммы Кэмпбелла
В постпроцессоре в настройках фильтра «Диаграмма Кэмпбелла» есть возможность изменить наклон критической линии и выбрать, каким образом будут определяться критические скорости:
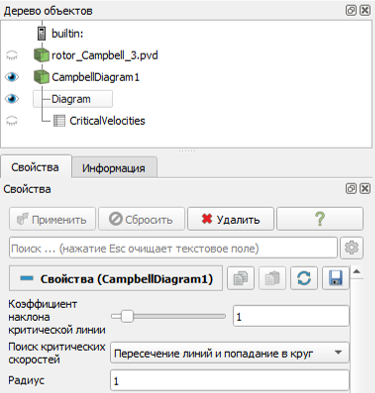
Рисунок 4. Настройки фильтра «Диаграмма Кэмпбелла» в постпроцессоре FidesysViewer
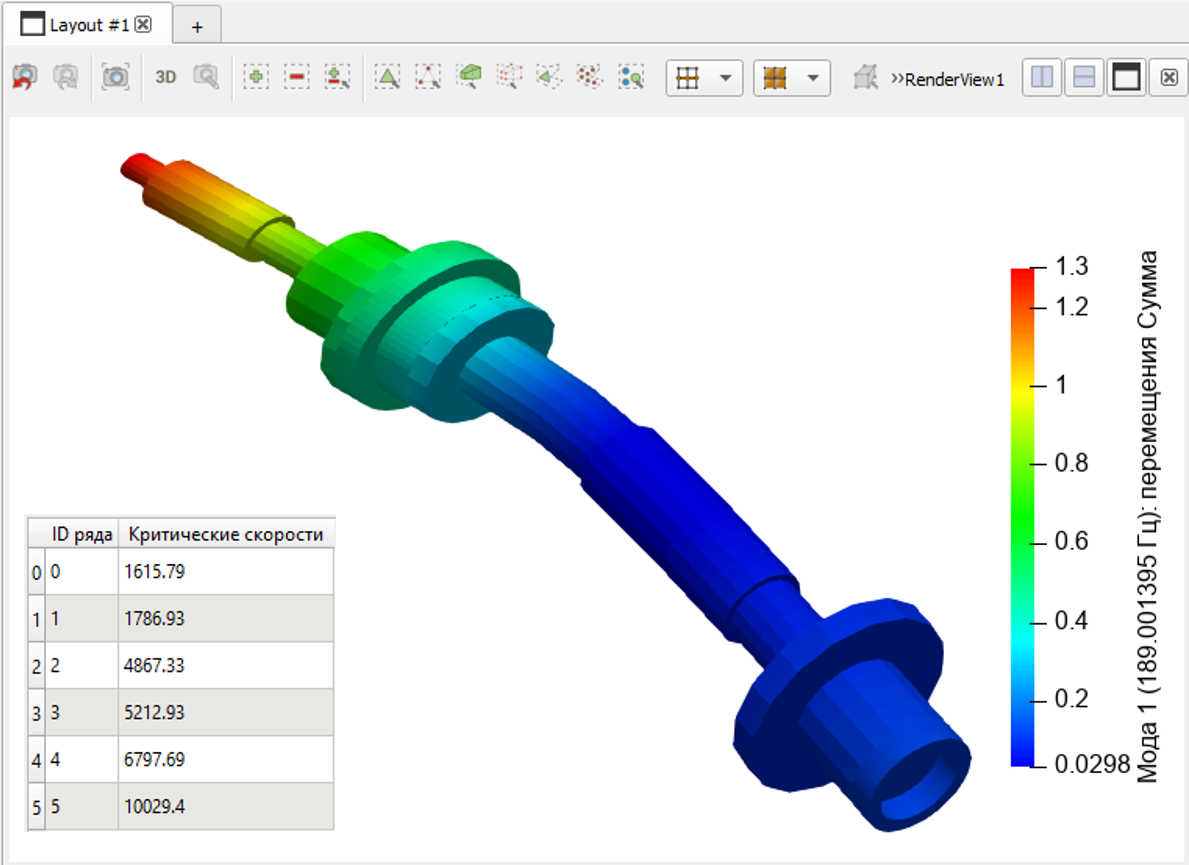
Рисунок 5. Значения критических скоростей и первая форма колебаний
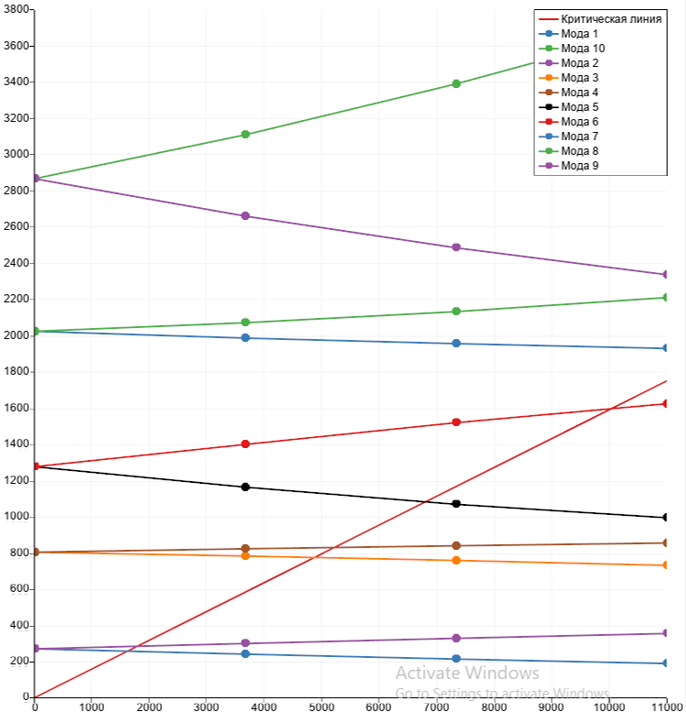
Рисунок 6. Диаграмма Кэмпбелла в постпроцессоре FidesysViewer
Упругопластический расчет для оболочечных элементов
Данный функционал долго находился на этапе тестирования, и его выпуск откладывался. Теперь в CAE Fidesys есть возможность проведения расчета напряженно-деформированного состояния конструкций, смоделированных оболочечными элементами в рамках упругопластической постановки, то есть после предела текучести в пластической области физико-механических свойств материала. В настоящий момент задание пластического поведения материала для оболочек доступно по теории течения Мизеса с изотропным упрочнением как по линейному закону, через тангенциальный модуль или предельные деформации, так и по точкам кривой напряжения/деформации. Учет больших перемещений и деформаций для оболочек пока не поддерживается.
Специалисты Группы «Борлас» подошли к вопросу изучения особенностей реализации данного функционала комплексно, с инженерной точки зрения. Во-первых, в примерах, которые идут в комплекте с установочным пакетом CAE Fidesys, есть тест NAFEMS:
Hinton E. Fundamental Tests for Two and Three-dimensional, Small Strain, Elastoplastic Finite Element Analysis / Emest Hinton, M.H. Ezatt. - NAFEMS, 1987.
В примере рассматривается плоская пластина в двумерной постановке. Для общего взгляда на реализацию упруго-пластического поведения оболочек в CAE Fidesys мы можем использовать данный пример, но перейти от пластины к моделированию оболочки.
Тест NAFEMS представляет собой пошаговое изменение формы пластины в 2D-постановке:
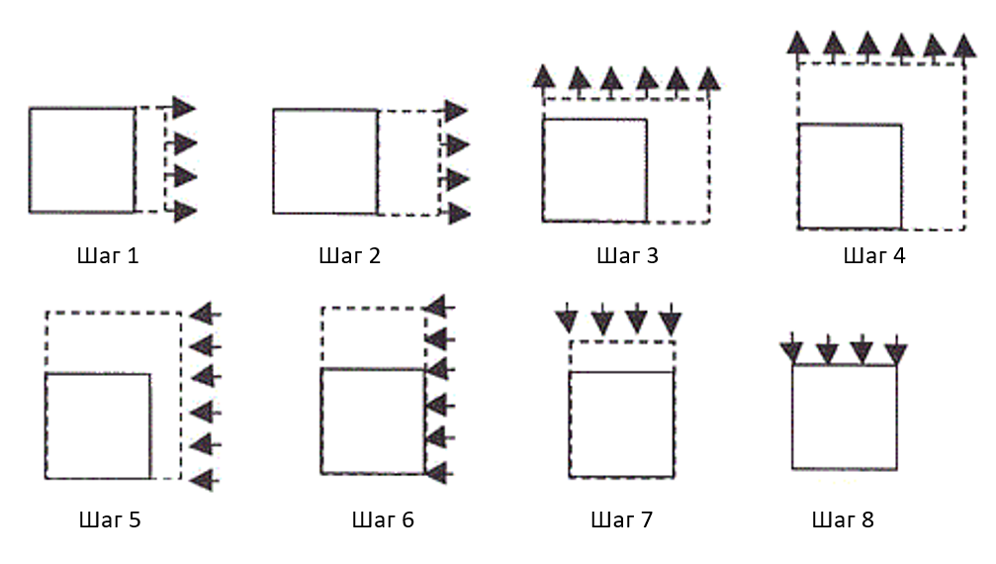
Рисунок 7. Шаги нагружения в тесте NAFEMS
Во-вторых, перед нами встает серьезная проблема: в тесте NAFEMS рассматривается плоское деформированное состояние пластины, а классическая теория оболочек построена на гипотезе плоских напряжений для тонких тел, то есть аналогия с плоским напряженным состоянием пластины.
Поэтому в нашем примере с оболочкой компоненты тензора напряжений и деформаций не будут совпадать с плоской задачей в тесте NAFEMS, но деформированная форма и перемещения – должны. Конечно, этого недостаточно для сравнения. Чтобы компенсировать недостающие данные, мы не будем проводить расчет в CAE Fidesys для плоского напряженного состояния пластины, с результатами которого на самом деле совпадают результаты оболочечной постановки. Мы посчитаем точно такую же задачу в ANSYS.
Ниже приводятся результаты сравнения с ANSYS по компонентам напряжений и деформаций (случай идеальной пластичности):
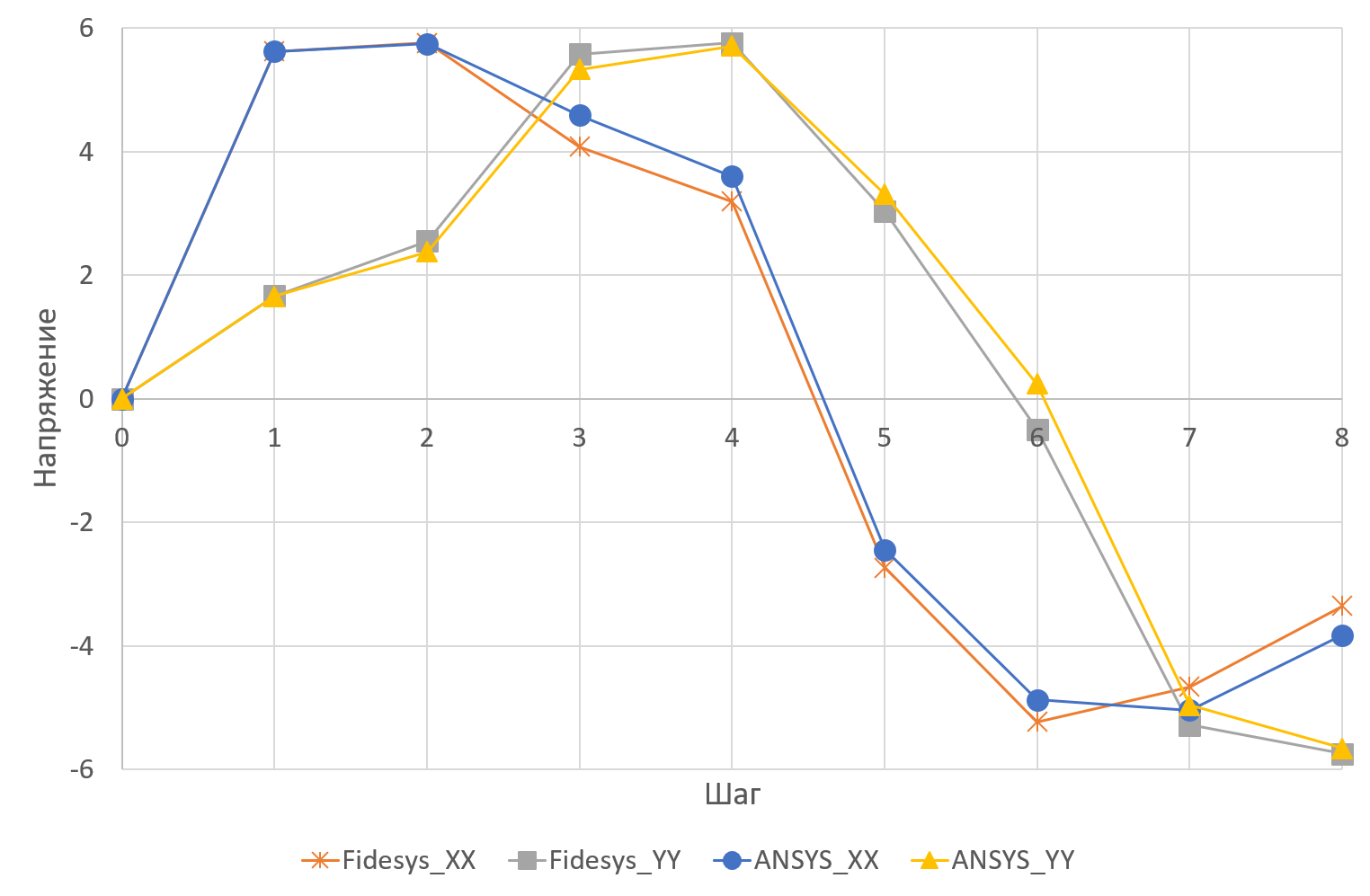
Рисунок 8. Сравнение напряжений CAE Fidesys и ANSYS
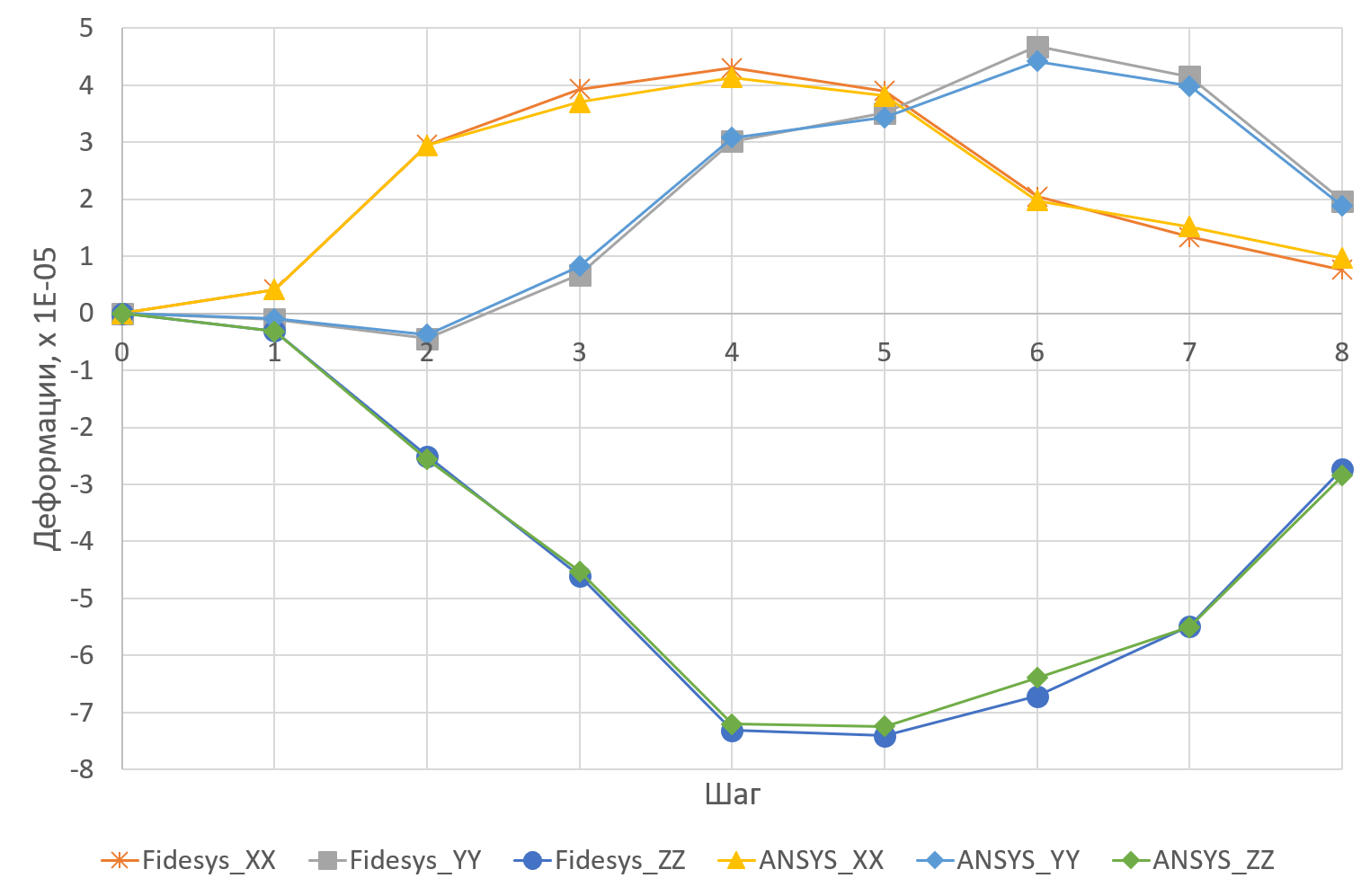
Рисунок 9. Сравнение деформаций CAE Fidesys и ANSYS
Cравнение с тестом NAFEMS в напряжениях по Мизесу говорит о том, что оболочечная постановка дает более качественную картину, чем плоская задача. Результат также совпадает с ANSYS.
Аналогичная картина сравнения получается в случае билинейного упрочнения.
Это касается теории тонких оболочек. Для случая толстых оболочек в CAE Fidesys можно применить обобщение для оболочки с квадратичным изменением по толщине, если моделировать оболочку методом спектральных элементов. Результат будет ближе к сеточно-сошедшемуся решению на твердотельных элементах, но это уже тема отдельной статьи.
Пользовательские сечения балок
В CAE Fidesys для работы с балочными элементами существует встроенная библиотека сечений. Но что делать, если в библиотеке нет необходимого сечения? До выхода версии 8.0 задать свойства произвольного сечения можно было вручную. Для этого они должны быть заранее известны.
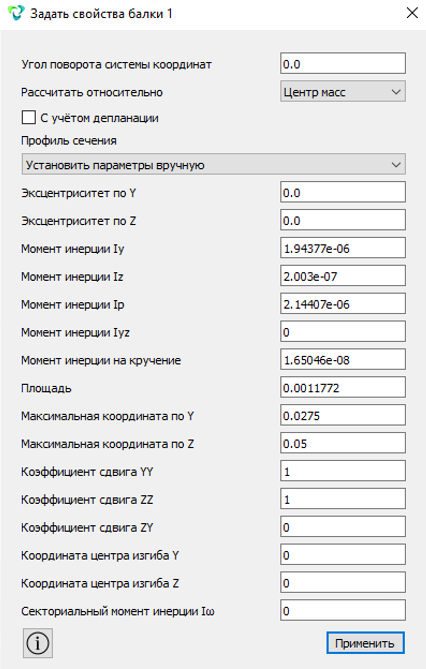
Рисунок 10. Задание свойств произвольного балочного сечения вручную
Отображение геометрии такого сечения было невозможно ни в препроцессоре, ни при обработке результатов расчета. Это было исключительно математическое описание.
С версии 8.0 появилась возможность использовать произвольные пользовательские сечения. Опция задания характеристик сечения вручную также доступна:
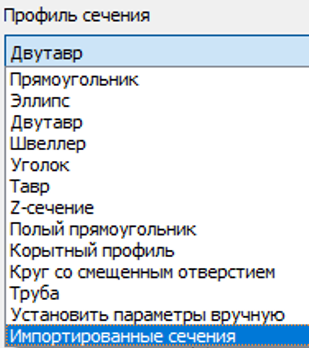
Рисунок 11. Новая опция задания свойств балочного сечения
Создать пользовательское сечение можно непосредственно в CAE Fidesys вручную, построив его геометрию или импортировав из доступных CAD-форматов. Важно, чтобы плоскость сечения лежала в плоскости XY.
На поверхности сечения необходимо построить конечно-элементную сетку. Количество узлов и элементов в сечении будут влиять на скорость расчета и, конечно, на точность результатов. Порядок элементов сечения не связан с порядком элементов самой балки или стержня, то есть балка может быть задана элементами с промежуточными узлами 2-го и выше порядков (спектральные элементы), а в сечении могут быть элементы только 1-го порядка без промежуточных узлов.
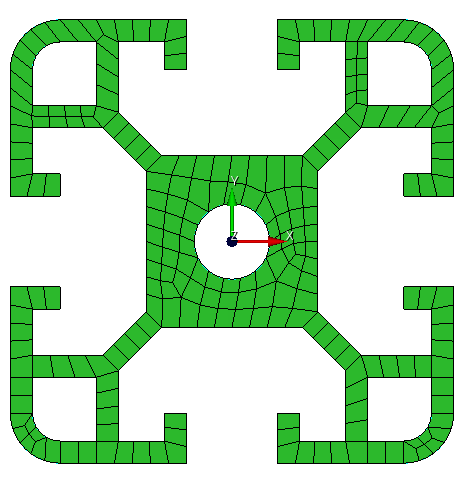
Рисунок 12. Конечно-элементная сетка пользовательского балочного сечения
Созданное сечение записывается в файл с расширением *.beam и имеет формат JSON; такой же формат имеет файл запуска на расчет в CAE Fidesys (расширение *.fc). Для сохранения сечения на Панели команд в Работе с блоками появилась новая функция – Пользовательское сечение.
Рисунок 13. Сохранение файла пользовательского балочного сечения
Если указать только название файла сечения в строке меню Имя файла, то сечение сохранится в системную папку CAE Fidesys. Обычно эта папка находится в директории пользователя Мои документы и называется CAE-Fidesys-<номер версии>. В данном случае – CAEFidesys-8.0. Это путь по умолчанию. При сохранении файла пользовательского сечения в системную папку это сечение автоматически становится доступно для выбора в инструменте задания сечения балочного элемента в пункте Импортированные сечения:
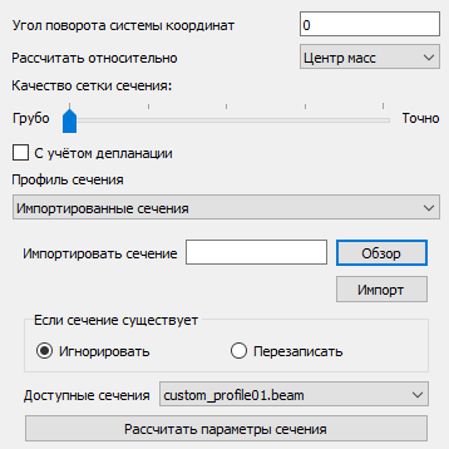
Рисунок 14. Выбор/импорт пользовательского балочного сечения
При сохранении файла сечения в любую другую директорию для его использования необходимо указать с помощью кнопки Обзор, где находится созданный файл, и импортировать пользовательское сечение с помощью кнопки Импорт. Эта процедура копирует ранее созданный файл поперечного сечения балочного элемента в системную папку CAE Fidesys, и в дальнейшем это сечение будет доступно для выбора в Импортированных сечениях до тех пор, пока пользователь не удалит файл этого сечения из системной папки CAE Fidesys.
Таким образом, можно сформировать библиотеку пользовательских сечений балочных элементов. Отображение балки в 3D-виде также теперь доступно при использовании пользовательских сечений:

Рисунок 15. Отображение балки с пользовательским сечением в препроцессоре CAE Fidesys 8.0
Пошаговый пример создания такого сечения можно найти на сайте fidesys-solvers.ru.
Конвертер Nastran BDF
В версии CAE Fidesys 8.0 был полностью переработан конвертер для импорта расчетных моделей и сеток из Nastran в формате BDF. В новой версии конвертера реализовано чтение материалов и свойств блоков – сечений балок и оболочек, расширен список поддерживаемых граничных условий и нагружений. Введена поддержка типов контактов Общий и Склейка.
Реализована конвертация систем координат – декартовы, цилиндрические, сферические.
При импорте BDF-файла Nastran в CAE Fidesys доступна опция Сохранять FC, которая позволяет сразу подготовить файл запуска на решение:
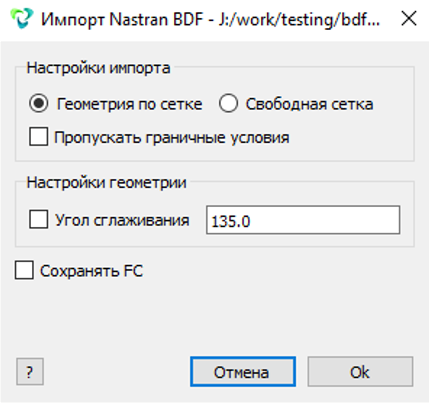
Рисунок 16. Интерфейс импорта Nastran BDF в препроцессоре CAE Fidesys 8.0
Типы конечных элементов Nastran, поддерживаемые в новом конвертере:
CTETRA, CHEXA, CPYRAM, CPENTA, CQUAD, CTRIA, CSHEAR, CBEAM, CBAR, CROD, CBUSH, CELAS2, CONM2.
В CAE Fidesys 8.0 поддерживаются следующие карты командного файла Nastran для задания граничных условий и нагружения:
SPC, SPC1, FORCE, MOMENT, RFORCE, GRAV, RBE1, RBE2, RBE3.
Типы моделей материалов Nastran, поддерживаемые в CAE Fidesys 8.0:
MAT1, MAT8, MAT10.
Анализ ошибок в расчетной модели
В CAE Fidesys 8.0 реализован новый инструмент Анализ модели, облегчающий пользователям работу с расчетной моделью до запуска на расчет и позволяющий получить информацию о возможных ошибках при создании модели или иных некорректных данных, которые могут повлиять на успешный запуск расчета.
Виджет Анализ модели находится на вкладке Инструменты:
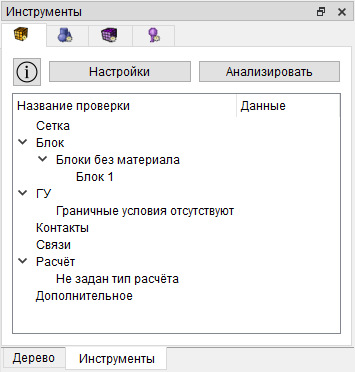
Рисунок 17. Инструмент «Анализ модели» в препроцессоре CAE Fidesys 8.0
Перечень проверок, которые доступны в версии 8.0, приведен на рис. 18:
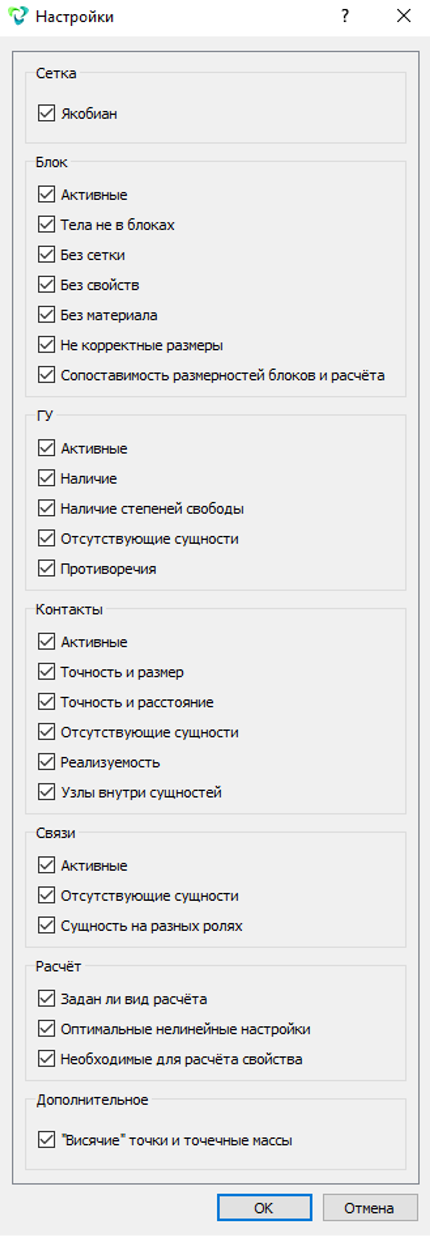
Рисунок 18. Настройки проверок в инструменте «Анализ модели»
Критерии прочности монослоя композиционного материала
Для оценки прочности композиционных материалов в постпроцессоре CAE Fidesys 8.0 реализованы следующие критерии прочности, которые базируются на предельных напряжениях монослоя:
- Критерий Цая-Хилла
- Критерий Хоффмана
- Критерий Цая-Ву
- Критерий Максимальных Напряжений
В постпроцессоре CAE Fidesys фильтр «Запас прочности композитов» позволяет вычислять запасы прочности в соответствии с данными критериями для многослойных оболочек, слои которых выполнены из ортотропных материалов. Фильтр «Запас прочности композитов» работает только с оболочечными конечными элементами. Используется допущение, что каждый монослой многослойной оболочки работает в условиях плоского напряженного состояния.
Данные критерии позволяют идентифицировать разрушение монослоя, но не прогнозируют различные формы разрушений, включая разрушение волокон и матрицы.
В фильтре есть возможность выбрать один или несколько необходимых критериев для оценки:
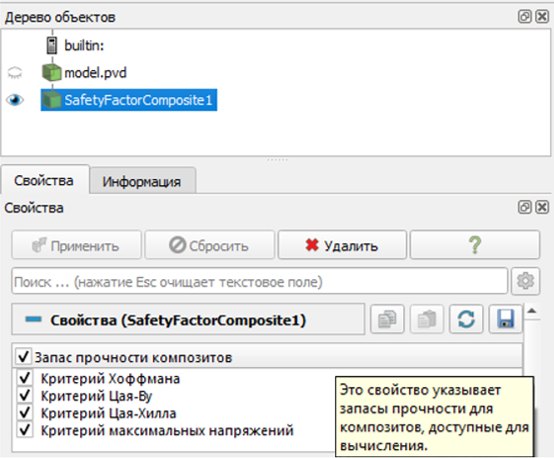
Рисунок 19. Выбор критериев прочности композитов для оценки в постпроцессоре FidesysViewer
На панели задач есть возможность выбрать слой для отображения, а в качестве компоненты можно выбрать критерий оценки запаса прочности.

Рисунок 20. Выбор требуемого критерия для отображения в постпроцессоре FidesysViewer
Минимум по всем слоям отображает результаты запасов прочности для слоя с минимальным критическим значением запаса прочности во всем пакете.
Подведем итоги. Восьмая версия CAE Fidesys получилась насыщенной новыми функциями и впечатляет объемом проделанной работы. После интеграции в предыдущей версии пакета модуля высоконелинейного анализа быстропротекающих процессов HSDF в CAE Fidesys 8.0 компания-разработчик продолжает наращивать темпы развития своего продукта, который все чаще становится основным инструментом для расчетов на предприятиях различных отраслей и эталонным инструментом для верификации расчетов, выполненных в других системах.